문제
방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 10 이하의 자연수이다.
입출력 예시
입력: 첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가 주어진다. 셋째 줄부터 E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수 (u, v, w)가 순서대로 주어진다. 이는 u에서 v로 가는 가중치 w인 간선이 존재한다는 뜻이다. u와 v는 서로 다르며 w는 10 이하의 자연수이다. 서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수도 있음에 유의한다.
출력: 첫째 줄부터 V개의 줄에 걸쳐, i번째 줄에 i번 정점으로의 최단 경로의 경로값을 출력한다. 시작점 자신은 0으로 출력하고, 경로가 존재하지 않는 경우에는 INF를 출력하면 된다.
입력예시1)
5 6
1
5 1 1
1 2 2
1 3 3
2 3 4
2 4 5
3 4 6출력예시1)
0
2
3
7
INF
코드
import heapq
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**6)
V, E = map(int, input().split())
start = int(input())
INF = int(1e9)
graph = [[] * (V + 1) for _ in range(V + 1)]
distance = [INF for _ in range(V + 1)]
for _ in range(E):
u, v, w = map(int, input().split())
graph[u].append((v, w))
def dijkstra():
q = []
heapq.heappush(q, (0, start))
distance[start] = 0
while q:
dist, now = heapq.heappop(q)
if distance[now] < dist: continue
for i in graph[now]:
cost = dist + i[1]
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0]))
dijkstra()
for i in range(1, V + 1):
if distance[i] == INF: print("INF")
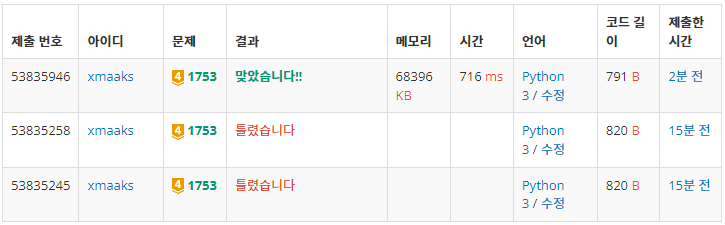
else: print(distance[i])실행 화면

채점 결과
728x90
'문제 풀이 > [BaekJoon]' 카테고리의 다른 글
| [BaekJoon] 2206 벽 부수고 이동하기 (Gold 3) - Python (0) | 2023.01.12 |
|---|---|
| [BaekJoon] 24416 알고리즘 수업 - 피보나치 수 1 (Bronze 1) - Python (0) | 2023.01.11 |
| [BaekJoon] 12865 평범한 배낭 (Gold 5) - Python (0) | 2023.01.10 |
| [BaekJoon] 13549 숨바꼭질 3 (Gold 5) - Python (0) | 2023.01.10 |
| [BaekJoon] 9935 문자열 폭발 (Gold 4) - Python (0) | 2023.01.10 |